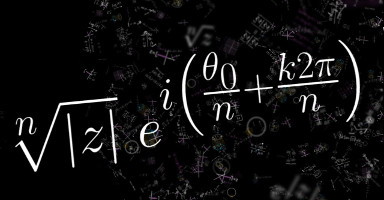Acerca de este curso

En este curso aprenderás a operar con números complejos al nivel requerido en los primeros cursos de grado de cualquier ingeniería, física o matemáticas.

El curso total intercala vídeos de teoría con resoluciones de ejercicios paso a paso. Podrás practicar con los ejercicios, con corección inmediata y luego practicar con las entrega de tareas y los exámenes de entrenamiento (dos parciales y un final). El curso monitorizará tus puntuaciones para que puedas valorar cómo progresas.

Muchos de los ejercicios que proponemos están al nivel de los de examen en un grado oficial. El curso incluye el libro de ejercicios con respuestas en formato PDF.

El curso completo consta de siete partes:

1. Operaciones elementales. Suma, resta, producto y cociente, con su interpretación geométrica. Módulo y argumento principal. Potencias. Fórmula de de Moivre.
2. Raíces, ramas y corte de ramificación. Funciones multivaluadas. Límites y continuidad.
3. Regiones del plano complejo. Conjugados. Desigualdades. Conjuntos abiertos, cerrados y conexos.
4. La función exponencial. Funciones inyectivas, sobreyectivas y biyectivas. Representación geométrica de la función exponencial.
5. La función logarítmica. Ramas y valor principal del logaritmo.
6. Transformaciones de Möbius.
7. Funciones analíticas. Funciones derivables, analíticas, holomorfas, armónicas y armónicas conjugadas.

• Apéndices: El curso concluye con tres secciones con una justificación para la identidad de Euler, una explicación del origen histórico de la unidad imaginaria y un repaso detallado del concepto de límite.